|
|
|||||||
|
|
Εργαλεία Θεμάτων | Τρόποι εμφάνισης |
|
#1
24-10-2013, 21:01
|
|||
|
|||
Βοήθεια σε συμφορουμίτη!!
Κατόπιν αιτήματος του γνωστού για τις ανησυχίες του συμφορουμίτη http://www.gsforum.gr/963659-post11.html
Σκέφτηκα να βοηθήσω έστω και λίγο, ελπίζοντας να δώσω διέξοδο και λίγη χαρά. Ας ευχηθούμε η στέρηση αυτή να είναι και η τελευταία... Giraffe Breeding and Reproduction Males are ready to mate when they are about 6 years of age. However, due to the way in which the stronger and more mature bulls get to mate first they don’t often get to at such an early age. In fact, it isn’t uncommon for them to be in there double digits of years before they are able to. You see, males that do get the right to mate will do so with an entire herd so there aren’t as many females to go around as it might seem. Females are ready to mate when they are about 4 years of age. What is really disgusting for most people is that the males will taste the urine of the females. This process will help him to discover which ones are ready to mate. They will be the ones with more estrus in their urine which is a type of hormone. The courting rituals of giraffes involve the gentle rubbing of their necks on each other. While giraffes have no set mating season it will usually take place during the rainy season. This is because they are less stressed out and because they have plenty of food to consume. When food supplies are very low then they have to kick into survival mode and they are less likely to take part in reproduction. This is also due to the fact that the females will only go into estrus when her needs are being met. In captivity though they are more likely to reproduce all throughout the year. This is due to the fact that they always have plenty of food and water available to them. This is one way to try to increase the number of giraffes out there but generally they aren’t in captivity for that purpose. It is believed that various species of giraffes have been able to successfully mate and have offspring in captivity but that doesn’t occur in the wild due to the different geographic locations. It takes approximately 15 months after conception for a giraffe calf to be born. Most of the time there is only one at a time but some reports of twins have been noted. The mother remains standing up when the baby drops from her body to the ground which is several feet below. The thick sac protecting the calf prevents it from being harmed during the birthing process. These aren’t small offspring by any means though as they are about 6 feet tall when they are born. They can also weigh about 150 pounds. In captivity they are a huge attraction for visitors. However, in the wild they are a threat to the entire herd as they will attract more predators to that group than normal. They can grow about 4 feet though during that first year of life. Amazingly, they learn how to walk within a couple of hours. However, they do get tired very fast and that means they can become easy pray too. For about two weeks the young calves will rest as much as they can and be protected by their mothers. Only about 25% of young giraffes make it to adulthood. This is mainly due to such predators while they are still in their infancy. The milk of the mother is very nutritious and the calves will drink from it for about the first year of life. Young giraffes feed from the grass and low lying leaves when they are about two months of age. They can do this standing underneath their mother while she feeds. In many herds though there are nurseries for the young to be protected while they mothers eat. That way they have the ability to produce enough milk for the young. Φυσικά υπάρχουν και άλλα είδη που χρήζουν ανάγκης. Συμπληρωματικά κάποια ενδιαφέροντα στοιχεία... ΠΟΛΙΤΙΚΗ ΑΝΘΡΩΠΟΛΟΓΙΑ ΤΟΥ "ΤΡΕΛΟΥ ΠΙΘΗΚΟΥ" Πολιτική Θρησκεία Φονταμενταλισμός  Ο πολιτισμός μας, αντί του «πάντων χρημάτων μέτρον είναι ο άνθρωπος» του Πρωταγόρα, προτίμησε το "παν μέτρον είναι το χρήμα των αγορών", όπου και αναδείχθηκε κυρίαρχα στα πεδία της ακαδημαϊκής, οικονομικής και πολιτικής σκέψης και θεωρίας. Οι κανόνες του χρήματος και της ιδιοκτησίας στάθηκαν πολλές φορές ανηλεείς μπροστά στον ανθρώπινο παράγοντα, εν ονόματι του αστού. Αυτό συνέβη, γιατί μια υβριδική ταξική ανθρωπολογία και πολιτισμική νεύρωση-ψύχωση, απέβη καθοριστική. Αντλεί τις δυνάμεις της από το αρχέγονο πηγάδι της ατέλειας, που αναδείχθηκε στην ανθρωπογένεση.[1] Αυτή η ατέλεια συμβολίζεται σε θρησκευτικές διηγήσεις και αρχαϊκούς μύθους.Αστοί ως συνήγοροι του ολοκληρωτισμού Ο αστός σταδιακά μεταμορφώνεται σε ένα τέρας ιδιοτέλειας και γίνεται η βάση για την νομιμοποίησή της. Πρόδρομοι του σύγχρονου αστού ήταν οι άνθρωποι της κοινωνίας του «άρτου και των θεαμάτων» στο Κολοσσαίο, οι διεφθαρμένοι αυτοκράτορες, Συγκλητικοί, Πραιτοριανοί, οι ασκούντες την ιερατική εξουσία και οι φεουδάρχες. Τί μεγάλη τιμή για την ανθρωπότητα! Επίσης, δυστυχώς πολλές φορές, οι καλλιτέχνες σμίλευσαν τον μόχθο της δουλείας -της πνευματικής και της σωματικής- των λαών για τα μνημεία τους και τα έργα τους και πολύ ορθά τα απαξιώνει στο έργο του «Γουόλντεν» ο Θορώ.[2] Όλοι οι άνθρωποι είναι εν δυνάμει αμετροεπείς αστοί και αυτό είναι ένα μεγάλο πρόβλημα. Αυτό συμβαίνει γιατί η αστική κυριαρχία είναι θέμα ανθρωπολογικού υποβάθρου. Ο άνθρωπος στον βαθμό που ακολουθεί την αμετροέπεια, χάνει την ευγενική μέση ατραπό. Τελικά μετατρέπεται σε τιτάνα ή θηρίο. Άλλοι τον έχουν βαπτίσει «τρελό πίθηκο». Αστοί ήταν οι άνθρωποι που παραδόθηκαν στη γοητεία της δύναμης των μαζικών κομματικών κοινωνιών, της λατρείας των ηγετών, των πογκρόμ και των γενοκτονιών των αντιφρονούντων. Αστοί ήταν όλοι οι συνήγοροι του ολοκληρωτισμού, και αυτό δείχνει η ανάλυση αυτών που συνοδοιπόρησαν -με την ψήφο τους- με τον Ναζισμό ή τον Φασισμό. Το ίδιο ισχύει και για αυτούς που, από τη νομενκλατούρα του υπαρκτού σοσιαλισμού, μεταλλάχτηκαν σε ηγέτες της πυραμίδας θεσμικής εκτροπής της αγοράς.[3] Ιστορικά παραδείγματα Ο αστός χωρίς μέτρο -δηλαδή χωρίς αρμονική εσωτερίκευση του λόγου και του κόσμου, χωρίς συνάφεια και συνέχεια, χωρίς αξιακή ή ιδεατή ιεραρχικότητα- ανέδειξε χαρακτηριστικά: i. την τερατουργηματική σκέψη ενός Νίτσε που γνώρισε την πολλαπλότητα της ταυτότητάς του ως τίμημα της απόλυτης χωριστικότητας ii. τον Ζαν Μπωντριγιάρ που ισορρόπησε μεταξύ μιας μηδενιστικής γοητείας και μιας κριτικής μετά-νεωτερικότητας iii. τους Μαρκήσιο Ντε Σαντ, Λεοπόλδο Μαζόχ και Ζωρζ Μπατάιγ με την αρέσκεια στην ανθρωποθυσία που θέλει να συντηρήσει τον κύκλο της απαγόρευσης για να υποστηρίξει τη λαγνεία και την εγκληματικότητά της iv. τους Ντε Μέστρ, Καρλ Σμιτ, Μπίσμαρκ, Ντίρινγκ και πληθώρα άλλων -σε διάφορες εποχές- επιχείρησαν την ανάδειξη μιας τιτανικής αντιποίησης του εαυτού και του κόσμου με τη μορφή μιας Μεγα-μηχανής[4] όπως θα έλεγε ο Αμερικανός φιλόσοφος Λιούις Μάμφορντ. Αυτή την προσπάθεια τιτανικής αντιποίησης του εαυτού και του κόσμου προσδιόρισε και οραματίστηκε ο Νίτσε, που είναι ο πιο ολοκληρωμένος εκφραστής του κακού[5] φτάνοντάς το σε "ύψη" υπέρτερα και του "Αγών μου". Ταυτόχρονα, αυτή η έλλειψη του μέτρου, αναδείχθηκε στην οικονομική προσωπικότητα της αργόσχολης τάξης.[6] Οι αναρχικοί, επίσης, έδειξαν ιδιαίτερες αντιφάσεις, με εξαίρεση την ευγενή φυσιογνωμία του Πέτρου Κροπότκιν, που υπήρξε ένας αστός με μέτρο. Ο Μιχαήλ Μπακούνιν ήταν εξαιρετικά αντιφατικός και δημοκόπησε, όπως αντίστοιχα και πολλοί καλλιτέχνες, με την ταλάντευση του στο άμετρο. Χαρακτηριστική ήταν η περίπτωση του Ιταλού ποιητή και συγγραφέα Ντ΄ Ανούντσιο Γκαμπριέλε, που έγινε σοβινιστικός πρωταγωνιστής των επεισοδίων της Τεργιέστης και συνεργός του φασισμού. Στην ιστορία αναπτύχθηκαν και αστοί όπως ο Ριχάρδος Βάγκνερ που έκλεισαν τον κύκλο της ζωής τους με έναν δραματικό ηρωισμό ψυχής, έχοντας περάσει ενδιάμεσα μέσα από τον εκτροχιασμό της αστικής ψυχολογίας. Ο δρόμος για το πνεύμα Δεν υπάρχει ένας βεβαιωμένος κανόνας για τον δρόμο του ανθρώπου προς το πνεύμα. Απαιτείται εξαιρετική διορατικότητα για να μπορεί να μιλήσει κανείς για την περιπέτεια της αναζήτησης του πνευματικού ορίζοντα ή του αθάνατου πνεύματος, όπως θα το αποκαλούσε ο εμπνευστής της Φαινομενολογίας, Γερμανός φιλόσοφος Έντμοντ Χούσερλ. Ο Ιταλός διευθυντής ορχήστρας Αρτούρο Τοσκανίνι, βαδίζοντας αυτό τον δρόμο, συγκρούστηκε με το φασιστικό καθεστώς του Μουσολίνι. Και άλλα επιμορφωτικά!!!! Θεώρημα των απείρων πιθήκων Από τη Βικιπαίδεια, την ελεύθερη εγκυκλοπαίδεια Μετάβαση σε: πλοήγηση, αναζήτηση  Αν δοθεί αρκετός χρόνος, ένας υποθετικός χιμπαντζής πληκτρολογώντας στην τύχη, θα παράξει ανάμεσα στα άλλα, σχεδόν σίγουρα και ένα από τα έργα του Σαίξπηρ. Σύμφωνα με το θεώρημα των απείρων πιθήκων, ένας πίθηκος που χτυπάει πλήκτρα στην τύχη σε μία γραφομηχανή για ένα άπειρο χρονικό διάστημα θα παράξει σχεδόν βέβαια ένα δεδομένο κείμενο όπως για παράδειγμα τα άπαντα του Ουίλιαμ Σαίξπηρ. Σε αυτό το πλαίσιο το «σχεδόν βέβαια» είναι μαθηματικός όρος με συγκεκριμένη έννοια, και ως «πίθηκος» δεν νοείται ένας πραγματικός πίθηκος, αλλά χρησιμοποιείται μεταφορικά ως μία αφηρημένη συσκευή που παράγει μία τυχαία σειρά γραμμάτων επ' άπειρον. Το θεώρημα καταδεικνύει τους κινδύνους στους συλλογισμούς για το άπειρο όταν υπεισέρχεται η υπόθεση τεράστιου αλλά πεπερασμένου αριθμού και αντίστροφα. Η πιθανότητα να παράξει ο πίθηκος ένα κείμενο με μέγεθος αντίστοιχο του Άμλετ, είναι τόσο μικρή ώστε αν το πείραμα εκτελούνταν, η πιθανότητα να συμβεί μέσα σε ένα χρονικό διάστημα της τάξης μεγέθους της ηλικίας του σύμπαντος είναι μηδαμινή αλλά όχι μηδενική. Παραλλαγές του θεωρήματος περιλαμβάνουν περισσότερους ή και άπειρους δακτυλογράφους, ενώ το κείμενο στόχος ποικίλει μεταξύ ολόκληρης βιβλιοθήκης και μίας μόνο πρότασης. Η ιστορία αυτών των θεωρημάτων ανιχνεύεται στο έργο του Αριστοτέλη Περὶ γενέσεως καὶ φθορᾶς και στο έργο του Κικέρωνα De natura deorum, εν συνεχεία στους Μπλεζ Πασκάλ και Τζόναθαν Σουίφτ, και τελικώς στα σύγχρονα θεωρήματα με τους εικονικούς γραφείς. Στις αρχές του 20ου αιώνα, ο Εμίλ Μπορέλ και ο Άρθουρ Έντιγκτον χρησιμοποίησαν το θεώρημα για να δείξουν τις χρονικές κλίμακες των θεμελίων της στατιστικής μηχανικής. Διάφοροι χριστιανοί απολογητές από την μία και ο Ρίτσαρντ Ντόκινς από την άλλη έχουν διαφωνήσει για την καταλληλότητα των πιθήκων ως μεταφορά για την εξέλιξη Το ενδιαφέρον του κοινού για τους πιθήκους που δακτυλογραφούν συντηρείται από τις πολλές εμφανίσεις του στην λογοτεχνία, την τηλεόραση, το ραδιόφωνο, την μουσική και το ίντερνετ. Το 2003 έγινε ένα πραγματικό πείραμα με μακάκους του είδους Macaca nigra. Το αποτέλεσμα της εργασίας τους ήταν πέντε σελίδες που αποτελούνταν κυρίως από το γράμμα 'S'.[1] Πίνακας περιεχομένων [Απόκρυψη]
Άμεση απόδειξη[Επεξεργασία | επεξεργασία κώδικα] Υπάρχει μια ευθεία απόδειξη του θεωρήματος. Αν δύο ενδεχόμενα είναι στατιστικά ανεξάρτητα, τότε η πιθανότητα να συμβούν και τα δύο ισούται με το γινόμενο των πιθανοτήτων να συμβεί το καθένα ξεχωριστά. Για παράδειγμα αν η πιθανότητα να βρέξει στο Μόντρεαλ μια συγκεκριμένη μέρα είναι 0.3 και η πιθανότητα να συμβεί σεισμός την ίδια μέρα στο Σαν Φρανσίσκο είναι 0.008 τότε η πιθανότητα να συμβούν και τα δύο είναι 0.3 × 0.008 = 0.0024. Έστω ότι η γραφομηχανή έχει 50 πλήκτρα, και η λέξη που πρέπει να γραφτεί είναι 'banana'. Δακτυλογραφώντας στην τύχη, η πιθανότητα το πρώτο γράμμα να είναι 'b' είναι 1/50, και η πιθανότητα το δεύτερο γράμμα να είναι 'a' είναι επίσης 1/50 κ.ο.κ, επειδή τα ενδεχόμενα είναι ανεξάρτητα. Έτσι, η πιθανότητα τα πρώτα έξι γράμματα να σχηματίσουν την λέξη 'μπανάνα' είναι (1/50) × (1/50) × (1/50) × (1/50) × (1/50) × (1/50) = (1/50)6, μικρότερη από ένα στα 15 δισεκατομμύρια. Για τον ίδιο λόγο, η πιθανότητα και τα 6 επόμενα γράμματα να σχηματίσουν την λέξη 'banana' είναι επίσης (1/50))6, κ.ο.κ. Από τα παραπάνω, η πιθανότητα να μην δακτυλογραφηθεί η λέξη banana σε ένα δεδομένο τμήμα 6 γραμμάτων είναι 1 − (1/50)6. Επειδή κάθε τμήμα δακτυλογραφείται ανεξάρτητα, η πιθανότητα Xn να μην δακτυλογραφηθεί μπανάνα σε κάθε ένα από τα πρώτα n τμήματα 6 γραμμάτων είναι 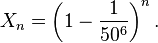 Καθώς το n αυξάνεται, το Xn γίνεται μικρότερο. Για n ένα εκατομμύριο, το Xn γίνεται περίπου 0.9999, αλλά για n 10 δισεκατομμύρια το Xn γίνεται περίπου 0.53 και για n 100 δισεκατομμύρια γίνεται περίπου 0.0017. Καθώς το n προσεγγίζει το άπειρο, η πιθανότητα Xn προσεγγίζει το μηδέν, που σημαίνει ότι για αρκετά μεγάλο n το Xn μπορεί να γίνει όσο μικρό είναι επιθυμητό.,[2][σημ. 1] και η πιθανότητα να δακτυλογραφηθεί μπανάνα προσεγγίζει το 100%.Ο ίδιος συλλογισμός δείχνει γιατί τουλάχιστον ένας από τους άπειρους πιθήκους θα παράξει ένα κείμενο όσο γρήγορα θα παράγονταν από έναν τέλεια ακριβή δακτυλογράφο που θα το αντέγραφε από το πρωτότυπο. Σε αυτή την περίπτωση Xn = (1 − (1/50)6)n όπου το Xn αναπαριστά την πιθανότητα ένας από τους πρώτους n πιθήκους να δακτυλογραφήσει banana σωστά στην πρώτη προσπάθεια. Αν θεωρήσουμε 100 δισεκατομμύρια πιθήκους, η πιθανότητα πέφτει στο 0.17%, και καθώς ο αριθμός των πιθήκων n αυξάνεται, η τιμή του Xn - η πιθανότητα των πιθήκων που θα αποτύχουν να παράξουν το δεδομένο κείμενο - προσεγγίζει το μηδέν/ Το όριο για το n να τείνει στο άπειρο είναι μηδέν. Ωστόσο, για οποιοδήποτε πλήθος πιθήκων με κάποιο τουλάχιστον φυσικό νόημα οι οποίοι να δακτυλογραφούν σε χρονικά διαστήματα με κάποιο τουλάχιστον φυσικό νόημα το αποτελέσματα είναι ανάποδο. Αν υπήρχαν τόσοι πίθηκοι όσα τα σωματίδια στο παρατηρήσιμο σύμπαν (1080), και καθένας από αυτούς δακτυλογραφούσε με ρυθμό 1.000 πλήκτρα ανά δευτερόλεπτο για χρόνο πάνω από 100 φορές την ηλικία του σύμπαντος (1020 seconds), η πιθανότητα να αναπαράγουν οι πίθηκοι ακόμα και ένα μικρό βιβλίο είναι σχεδόν μηδενική. Δείτε Πιθανότητες, παρακάτω. Άπειρες συμβολοσειρές[Επεξεργασία | επεξεργασία κώδικα] Οι δύο προτάσεις παραπάνω μπορούν αν εκφραστούν πιο γενικά και πιο συνεπτυγμένα με όρους συμβολοσειρών, οι οποίες είναι ακολουθίες χαρακτήρων επιλεγμένες από ένα πεπερασμένο αλφάβητο:
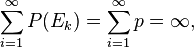 η πιθανότητα ότι άπειρα από τα Ek θα εφανιστούν είναι 1. Το πρώτο θεώρημα αποδεικνύεται αναλόγως. Μπορεί κανείς να χωρίσει την τυχαία συμβολοσειρά σε μη αλληλεπικαλυπτόμενα τμήματα που να ταιριάζουν στο μέγεθος του επιθυμητού κειμένου, και να κάνει Ek το ενδεχόμενο όπου το kστο τμήμα ισούται με την επιθυμητή συμβολοσειρά.[σημ. 2]Πιθανότητες[Επεξεργασία | επεξεργασία κώδικα] Αγνοώντας την στίξη, τα διαστήματα και τα κεφαλαία, ένας πίθηκος που δακτυλογραφεί τυχαία με κανονική κατανομή έχει πιθανότητα μία στις 26 να δακτυλογραφήσει σωστά το πρώτο γράμμα από τον Άμλετ. Έχει πιθανότητα μία στις 676 (26 × 26) να δακτυλογραφήσει τα πρώτα δύο γράμματα. Επειδή η πιθανότητα μειώνεται εκθετικά, στα είκοσι γράμματα είναι ήδη ένα στα 2620 = 19,928,148,895,209,409,152,340,197,376 (σχεδόν 2 × 1028). Για την περίπτωση ολόκληρου του κειμένου του Άμλετ, η πιθανότητα είναι υπερβολικά μικρή ώστε να γίνει αντιληπτή σε ανθρώπινους όρους. Το κείμενο του Άμλετ περιέχει περίπου 130.000 γράμματα.[σημ. 3] Έτσι η πιθανότητα είναι ένα στα 3.4 × 10183,946 ώστε να δακτυλογραφηθεί σωστά το κείμενο στην πρώτη προσπάθεια. Ο μέσος αριθμός γραμμάτων που χρειάζεται να δακτυλογραφηθεί μέχρι να εμφανιστεί το κείμενο είναι επίσης 3.4 × 10183,946,[σημ. 4] ή συμπεριλαμβάνοντας και την στίξη, 4.4 × 10360,783.[σημ. 5] Ακόμα και αν το παρατηρήσιμο σύμπαν ήταν γεμάτο πιθήκους που δακτυλογραφούσαν όλη την ώρα, η συνολική πιθανότητα να παράξουν ένα αντίγραφο του Άμλετ θα ήταν 1 / 10183,800. Όπως το έθεσαν ο Τσαρλς Κάιτελ και ο Χέρμπερτ Κρέμερ, «η πιθανότητα για τον Άμλετ είναι έτσι μηδέν υπό οποιαδήποτε επιχειρησιακή έννοια…», και η πρόταση ότι οι πίθηκοι πρέπει τελικώς να πετύχουν «δίνει παραπλανητικό συμπέρασμα για τους πολύ μεγάλους αριθμούς.» Αυτό προέρχεται από το εγχειρίδιο τους στην θερμοδυναμική, το πεδίο του οποίου το στατιστικό υπόβαθρο έδωσε το κίνητρο για τις πρώτες γνωστές εμφανίσεις της υπόθεσης των πιθήκων που δακτυλογραφούν.[3] Ιστορία[Επεξεργασία | επεξεργασία κώδικα] Στατιστική μηχανική[Επεξεργασία | επεξεργασία κώδικα] Μία από τις μορφές που είναι γνωστό σήμερα το θεώρημα, με τους πίθηκους που δακτυλογραφούν, εμφανίστηκε στο άρθρο του Εμίλ Μπορέλ Mécanique Statistique et Irréversibilité (1913, Στατιστική μηχανική κα μη αναστρεψιμότητα),),[4] και στο βιβλίο του, Le Hasard (1914). Οι πίθηκοί του δεν είναι πραγματικοί, αλλά μία μεταφορά για ένα φανταστικό τρόπο να παραχθεί μία μεγάλη, τυχαία ακολουθία γραμμάτων. Ο Μπορέλ έγραψε ότι αν ένα εκατομμύριο πίθηκοι δακτυλογραφούσαν για δέκα ώρες την ημέρα, θα ήταν εξαιρετικά απίθανο το έργο τους να περιέχει ακριβώς όλα τα βιβλία των πλουσιότερων βιβλιοθηκών του κόσμου, και όμως, για σύγκριση, ήταν ακόμα πιο απίθανο από αυτό οι νόμοι της στατιστικής μηχανικής να παραβιαστούν, έστω και για σύντομο διάστημα. Ο φυσικός Άρθουρ Έντιγκτον προχώρησε την σκέψη του Μπορέλ παραπέρα στο έργο του Nature of the Physical World (Η Φύση του Φυσικού Κόσμου, 1928), γράφοντας: Αν αφήσω τα δάκτυλά μου να περιπλανηθούν άσκοπα στα πλήκτρα μιας γραφομηχανής μπορεί να συμβεί το κείμενό μου να είναι μία πρόταση με νόημα. Αν μία στρατιά πιθήκων χτυπούσαν πλήκτρα σε γραφομηχανές μπορεί να έγραφαν όλα τα βιβλία του Βρετανικού Μουσείου. Η πιθανότητα να το πετύχουν αυτό είναι σαφώς μεγαλύτερη από αυτήν των μορίων να επιστρέψουν στο ένα μισό του δοχείου.[5]Με αυτά τα παραδείγματα ο αναγνώστης καλούνταν να αναλογιστεί την τεράστια απιθανότητα η εργασία μεγάλου αλλά πεπερασμένου αριθμού πιθήκων για μεγάλο αλλά πεπερασμένο χρονικό διάστημα να έχει αποτέλεσμα ένα σημαντικό έργο με την ακόμη μεγαλύτερη απιθανότητα συγκεκριμένων φυσικών φαινομένων. Κάθε φυσική διεργασία που είναι πιο απίθανο να συμβεί από την επιτυχία τέτοιων πιθήκων θεωρείται πρακτικώς απίθανη, και μπορεί να ειπωθεί με ασφάλεια ότι δεν πρόκειται να συμβεί ποτέ.[3] Προέλευση και «Η Ολική Βιβλιοθήκη»[Επεξεργασία | επεξεργασία κώδικα] Σε ένα δοκίμιο του 1939 με τίτλο «Η Ολική Βιβλιοθήκη» (The Total Library), ο Αργεντίνος συγγραφέας Χόρχε Λουίς Μπόρχες, εντόπισε την προέλευση της έννοιας των άπειρων πιθήκων στα Μεταφυσικά του Αριστοτέλη. Εξηγώντας τις αντιλήψεις του Λεύκιππου, κατά τον οποίο ο κόσμος προήλθε από τυχαίους συνδυασμούς ατόμων, ο Αριστοτέλης σημείωσε ότι τα άτομα αυτά καθεαυτά είναι ομογενή και ότι οι πιθανές διατάξεις τους διαφέρουν μόνο στο σχήμα, την θέση και την διάταξη. Στο έργο του, Περί γενέσεως και φθοράς, συγκρίνει με αυτό τον τρόπο με τον οποίο μια τραγωδία και μια κωμωδία αποτελείται από τα ίδια «άτομα», δηλαδή αλφαβητικούς χαρακτήρες.[6] Τρεις αιώνες αργότερα, ο Κικέρωνας στο έργο του De natura deorum (Περί της φύσεως των θεών) διαφώνησε με την ατομική κοσμοθεώρηση: Αυτός ο οποίος το πιστεύει αυτό μπορεί επίσης να πιστεύει ότι αν μία μεγάλη ποσότητα από τα εικοσιένα γράμματα, φτιαγμένα είτε από χρυσό είτε από άλλη ύλη, πετιόνταν στο έδαφος, θα έπεφταν με τέτοιο τρόπο ώστε να σχηματίσουν τα Χρονικά του Έννιου. Αμφιβάλω αν η τύχη θα μπορούσε να φτιάξει έστω ένα στίχο από αυτά.[7]Ο Μπόρχες ακολουθεί την ιστορία αυτού του επιχειρήματος εν συνεχεία στον Μπλεζ Πασκάλ και τον Τζόναθαν Σουίφτ, και παρατηρεί ότι στον καιρό του το λεξιλόγιο είχε αλλάξει. Το 1939, ο ιδιωματισμός ήταν «ότι μισή ντουζίνα πίθηκοι με γραφομηχανές θα μπορούσαν, σε μερικές αιωνιότητες να παράξουν όλα τα βιβλία του Βρετανικού Μουσείου» (Στο ο οποίο ο Μπόρχες προσέθεσε, «ένας αθάνατος πίθηκος θα αρκούσε.») Ο Μπόρχες κατόπιν φαντάζεται τα περιεχόμενα της Ολικής Βιβλιοθήκης τα οποία θα παράγονταν από αυτή την επιχείρηση στην πλήρη έκτασή της: Τα πάντα: η αναλυτική ιστορία του μέλλοντος, οι Αιγύπτιοι του Αισχύλου, ο ακριβής αριθμός των φορών που τα νερά του Γάγγη αντικατόπτρισαν την πτήση ενός γερακιού, η μυστική και αληθινή φύση της Ρώμης, η εγκυκλοπαίδεια Novalis θα είχε κατασκευάσει τα όνειρά και ημι-όνειρα μου της αυγής της 14ης Αυγούστου 1934, την απόδειξη του θεωρήματος του Φερμά, τα άγραφα κεφάλαια του Edwin Drood, τα ίδια κεφάλαια μεταφρασμένα στην γλώσσα που μιλούν οι Γαράμαντες, τα παράδοξα που εφηύρε ο Μπέρκλεϊ για τον Χρόνο αλλά δεν δημοσίευσε, τα βιβλία του σιδήρου του Urizen, τις πρόωρες εμπνεύσεις του Stephen Dedalus, οι οποίες θα ήταν χωρίς νόημα πριν από ένα κύκλο χιλίων χρόνων, το γνωστικό Ευαγγέλιο του Βασιλίδη, το τραγούδι που τραγούδησαν οι Σειρήνες, ο πλήρης κατάλογος της Βιβλιοθήκης, η απόδειξη ανακρίβειας αυτού του καταλόγου. Τα πάντα: αλλά για κάθε γραμμή με νόημα ή ακριβούς δεδομένου θα υπήρχαν εκατομμύρια κακοφωνίες χωρίς νόημα, φραστικά συνονθυλεύματα και ανοησίες. Τα πάντα: αλλά όλες οι γενιές της ανθρωπότητας θα μπορούσαν να περάσουν από τα ιλιγγιώδη ράφια, ράφια που εξαλείφουν την μέρα και στα οποία βρίσκεται το χάος, για να ανταμειφθούν με μία ανεκτή σελίδα.[8]Η έννοια της ολικής βιβλιοθήκης του Μπόρχες ήταν το κύριο θέμα του δημοφιλούς βιβλίου του «Η Βιβλιοθήκη της Βαβέλ» (1941), στο οποίο περιγράφεται μία αφάνταστα τεράστια βιβλιοθήκη η οποία αποτελείται από συμπλεγμένες εξαγωνικές αίθουσες, που μαζί περιέχουν όλους τους πιθανούς τόμους που θα μπορούσαν να συντεθούν από τα γράμματα του αλφαβήτου και μερικούς χαρακτήρες στίξης. Last edited by yannis; 24-10-2013 at 21:02. |
|
|
Threaded Mode